Zeta potential is a physical property which is exhibited by any particle in suspension, macromolecule or material surface. It can be used to optimize the formulations of suspensions, emulsions and protein solutions, predict interactions with surfaces, and optimize the formation of films and coatings. Knowledge of the zeta potential can reduce the time needed to produce trial formulations. It can also be used as an aid in predicting long-term stability.
The measurement of macromolecule charge, or more specifically protein charge, requires a very sensitive system, such as the new Zetasizer ZSP, and a technique to reduce the sample volume requirement, and avoid sample degradation. This system and technique are described in MRK1846.
The measurement of the zeta potential of surfaces requires an accessory for the Zetasizer Nano, and the subject and accessory are described separately in document MRK1749.
This introduction concentrates on the zeta potential of colloidal systems, with a density low enough such that if they remain dispersed, sedimentation is negligible.
Three of the fundamental states of matter are solids, liquids and gases. If one of these states is finely dispersed in another then we have a 'colloidal system'. These materials have special properties that are of great practical importance.
There are various examples of colloidal systems that include aerosols, emulsions, colloidal suspensions and association colloids.
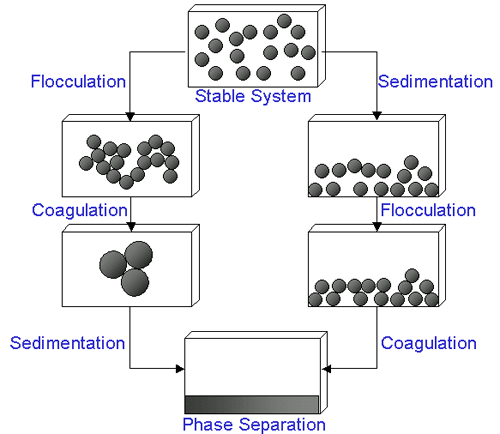
In certain circumstances, the particles in a dispersion may adhere to one another and form aggregates of successively increasing size, which may settle out under the influence of gravity. An initially formed aggregate is called a floc and the process of its formation flocculation. The floc may or may not sediment or phase separate. If the aggregate changes to a much denser form, it is said to undergo coagulation. An aggregate usually separates out either by sedimentation (if it is more dense than the medium) or by creaming (if it less dense than the medium). The terms flocculation and coagulation have often been used interchangeably. Usually, coagulation is irreversible whereas flocculation can be reversed by the process of deflocculation. Figure 1 schematically represents some of these processes.
|
The scientists Derjaguin, Verwey, Landau and Overbeek developed a theory in the 1940s which dealt with the stability of colloidal systems. DVLO theory suggests that the stability of a particle in solution is dependent upon its total potential energy function VT. This theory recognizes that VT is the balance of several competing contributions:
VT = VA + VR + VS
VS is the potential energy due to the solvent, it usually only makes a marginal contribution to the total potential energy over the last few nanometers of separation. Much more important is the balance between VA and VR, these are the attractive and repulsive contributions. They potentially are much larger and operate over a much larger distance.
VA = -A/(12 π D2)
where A is the Hamaker constant and D is the particle separation.
The repulsive potential VR is a far more complex function.
VR = 2 π ε a ζ2 exp(-κD)
where a is the particle radius, π is the solvent permeability, κ is a function of the ionic composition and ζ is the zeta potential.
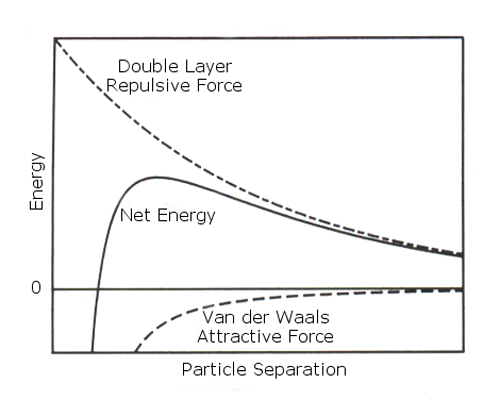
DVLO theory suggests that the stability of a colloidal system is determined by the sum of these van der Waals attractive (VA) and electrical double layer repulsive (VR) forces that exist between particles as they approach each other due to the Brownian motion they are undergoing. Figure 2a shows the separate forces as a dotted line, and the sum of these forces as the solid line. This sum has a peak, and the theory proposes that particles that are initially separated are prevented from approaching each other because of the repulsive force. However if the particles are forced with sufficient energy to overcome that barrier, for example by increasing the temperature, the attractive force will pull them into contact where they adhere strongly and irreversibly together.
|
Therefore if the particles have a sufficiently high repulsion, the dispersion will resist flocculation and the colloidal system will be stable. However if a repulsion mechanism does not exist then flocculation or coagulation will eventually take place.
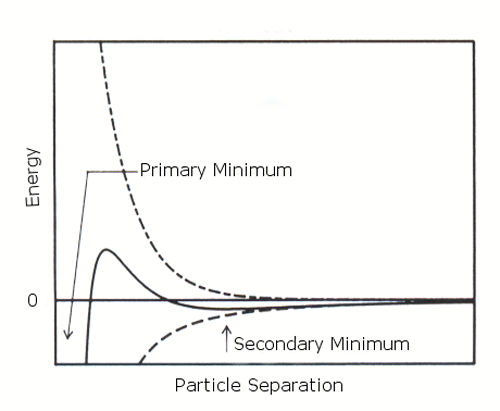
If the zeta potential is reduced (e.g. in high salt concentrations), there is a possibility of a "secondary minimum" being created, where a much weaker and potentially reversible adhesion between particles exists (figure 2 (b)). These weak flocs are sufficiently stable not to be broken up by Brownian motion, but may disperse under an externally applied force such as vigorous agitation.
|
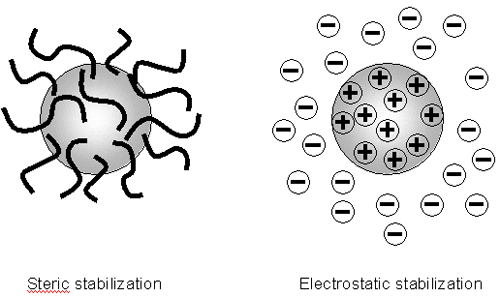
Therefore to maintain the stability of the colloidal system, the repulsive forces must be dominant. How can colloidal stability be achieved? There are two fundamental mechanisms that affect dispersion stability (figure 3):
|
Each mechanism has its benefits for particular systems. Steric stabilization is simple, requiring just the addition of a suitable polymer. However it can be difficult to subsequently flocculate the system if this is required, the polymer can be expensive and in some cases the polymer is undesirable e.g. when a ceramic slip is cast and sintered, the polymer has to be 'burnt out'. This causes shrinkage and can lead to defects.
Electrostatic or charge stabilization has the benefits of stabilizing or flocculating a system by simply altering the concentration of ions in the system. This is a reversible process and is potentially inexpensive.
It has long been recognized that the zeta potential is a very good index of the magnitude of the interaction between colloidal particles and measurements of zeta potential are commonly used to assess the stability of colloidal systems.
Most colloidal dispersions in aqueous media carry an electric charge. There are many origins of this surface charge depending upon the nature of the particle and its surrounding medium, here we will consider the more important mechanisms.
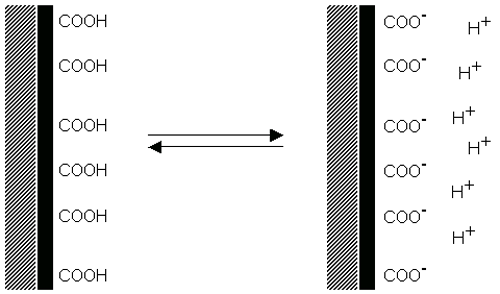
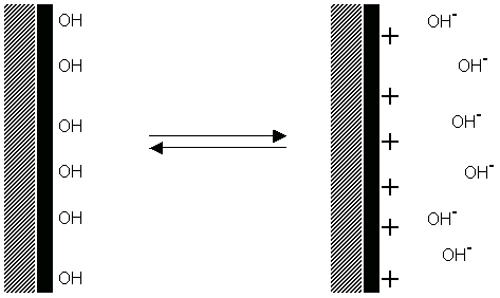
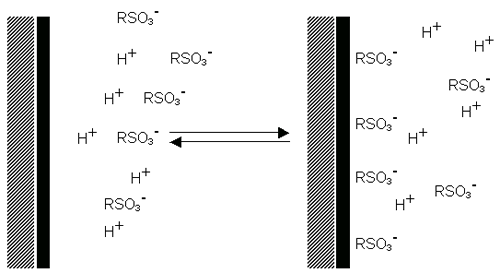
Dissociation of acidic groups on the surface of a particle will give rise to a negatively charged surface. Conversely, a basic surface will take on a positive charge (figure 4). In both cases, the magnitude of the surface charge depends on the acidic or basic strengths of the surface groups and on the pH of the solution. The surface charge can be reduced to zero by suppressing the surface ionization by decreasing the pH in case of negatively charged particles (figure 4(a)) or by increasing the pH in the case of positively charged particles (figure 4(b)).
|
|
Differential loss of ions from the crystal lattice
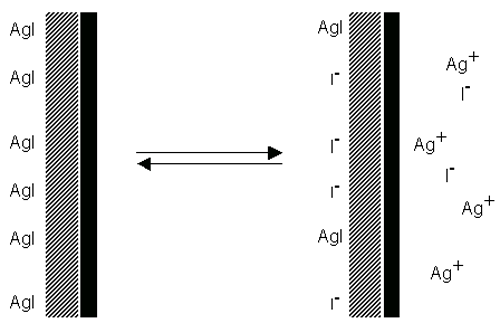
As an example, consider a crystal of silver iodide placed in water. Solution of ions occurs. If equal amounts of Ag+ and I- ions were to dissolve, the surface would be uncharged. In fact silver ions dissolve preferentially, leaving a negatively charged surface (figure 5). If Ag+ ions are now added the charge falls to zero. Further addition leads to a positively charged surface.
|
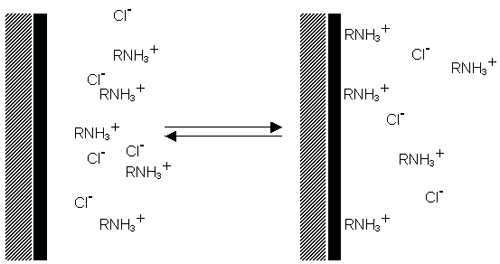
Surfactant ions may be specifically adsorbed on the surface of a particle, leading, in the case of cationic surfactants, to a positively charged surface (figure 6(a)) and, in the case of anionic surfactants, to a negatively charged surface (figure 6(b)).
|
|
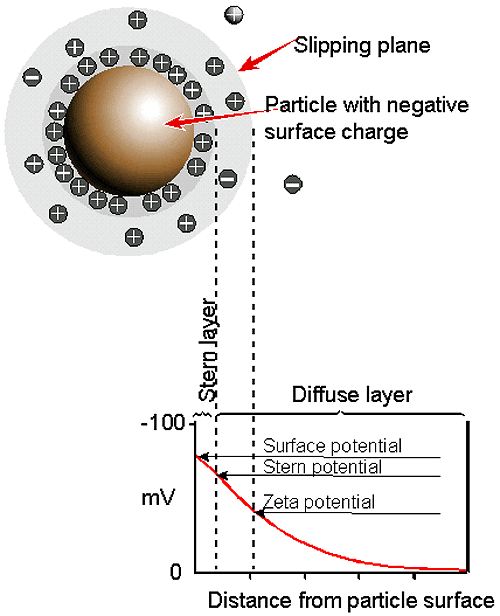
The development of a net charge at the particle surface affects the distribution of ions in the surrounding interfacial region, resulting in an increased concentration of counter ions, ions of opposite charge to that of the particle, close to the surface. Thus an electrical double layer exists round each particle.
The liquid layer surrounding the particle exists as two parts; an inner region (Stern layer) where the ions are strongly bound and an outer (diffuse) region where they are less firmly associated. Within the diffuse layer there is a notional boundary inside which the ions and particles form a stable entity. When a particle moves (e.g. due to gravity), ions within the boundary move it. Those ions beyond the boundary stay with the bulk dispersant. The potential at this boundary (surface of hydrodynamic shear) is the zeta potential (figure 7).
|
The magnitude of the zeta potential gives an indication of the potential stability of the colloidal system. If all the particles in suspension have a large negative or positive zeta potential then they will tend to repel each other and there will be no tendency for the particles to come together. However, if the particles have low zeta potential values then there will be no force to prevent the particles coming together and flocculating.
The general dividing line between stable and unstable suspensions is generally taken at either +30 or -30 mV. Particles with zeta potentials more positive than +30 mV or more negative than -30 mV are normally considered stable. However, if the particles have a density greater than the dispersant, even though they are dispersed, they will eventually sediment forming a close packed bed (i.e. a hard cake).
Thus it can be seen that as the zeta potential depends on the nature of the dispersant as well as the surface, The zeta potential of a particle must include the definition of the nature of the dispersant as well, if the zeta potential of different materials is to be compared.
The main parameters of the system are considered here.
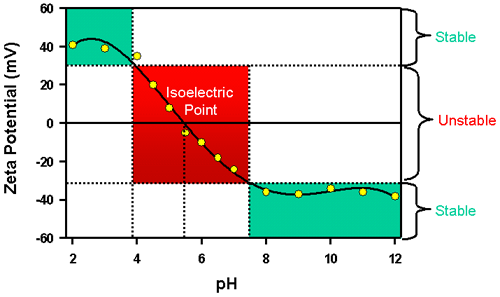
In aqueous media, the pH of the sample is one of the most important factors that affects its zeta potential. Imagine a particle in suspension with a negative zeta potential. If more alkali is added to this suspension then the particles tend to acquire more negative charge. If acid is added to this suspension then a point will be reached where the charge will be neutralized. Further addition of acid may cause a build up of positive charge if the ions are specifically adsorbed. In this case a zeta potential versus pH curve will be positive at low pH and lower or negative at high pH. The point where the plot passes through zero zeta potential is called the isoelectric point and is very important from a practical consideration. It is normally the point where aggregation is most likely and hence the colloidal system is least stable.
A typical plot of zeta potential versus pH is shown in figure 8. In this example, the isoelectric point of the sample is at approximately pH 5.5. In addition, the plot can be used to predict that the sample should be stable at pH values less than 4 (sufficient positive charge is present) and greater than pH 7.5 (sufficient negative charge is present). Problems with dispersion stability would be expected at pH values between 4 and 7.5 as the zeta potential values are between +30 and -30mV.
|
The thickness of the double layer (κ-1) depends upon the concentration of ions in solution and can be calculated from the ionic strength of the medium. The higher the ionic strength, the more compressed the double layer becomes. The valency of the ions will also influence double layer thickness. A trivalent ion such as Al3+ will compress the double layer to a greater extent in comparison with a monovalent ion such as Na+.
Inorganic ions can interact with charged surfaces in one of two distinct ways (i) non-specific ion adsorption where they have no effect on the isoelectric point. (ii) specific ion adsorption, which will lead to a change in the value of the isoelectric point. The specific adsorption of ions onto a particle surface, even at low concentrations, can have a dramatic effect on the zeta potential of the particle dispersion. In some cases, specific ion adsorption can lead to charge reversal of the surface.
The effect of the concentration of a formulation component on the zeta potential can give information to assist in formulating a product to give maximum stability. The influence of known contaminants on the zeta potential of a sample can be a powerful tool in formulating the product to resist flocculation for example.
An important consequence of the existence of electrical charges on the surface of particles is that they interact with an applied electric field. These effects are collectively defined as electrokinetic effects. There are four distinct effects depending on the way in which the motion is induced. These are:
Electrophoresis: the movement of a charged particle relative to the liquid it is suspended in under the influence of an applied electric field
Electroosmosis: the movement of a liquid relative to a stationary charged surface under the influence of an electric field
Streaming potential: the electric field generated when a liquid is forced to flow past a stationary charged surface
Sedimentation potential: the electric field generated when charged particles sediment
When an electric field is applied across an electrolyte, charged particles suspended in the electrolyte are attracted towards the electrode of opposite charge. Viscous forces acting on the particles tend to oppose this movement. When equilibrium is reached between these two opposing forces, the particles move with constant velocity.
The velocity is dependent on the strength of electric field or voltage gradient, the dielectric constant of the medium, the viscosity of the medium and the zeta potential.
The velocity of a particle in a unit electric field is referred to as its electrophoretic mobility. Zeta potential is related to the electrophoretic mobility by the Henry equation:-
UE = 2 ε z f(κa)
3η
where UE = electrophoretic mobility, z = zeta potential, ε = dielectric constant, η = viscosity and f(κa) = Henry's function.
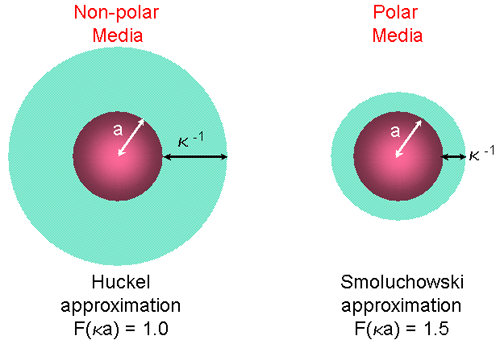
The units of κ, termed the Debye length, are reciprocal length and κ-1 is often taken as a measure of the "thickness" of the electrical double layer. The parameter 'a' refers to the radius of the particle and therefore κa measures the ratio of the particle radius to electrical double layer thickness (figure 9). Electrophoretic determinations of zeta potential are most commonly made in aqueous media and moderate electrolyte concentration. F(κa) in this case is 1.5, and this is referred to as the Smoluchowski approximation. Therefore calculation of zeta potential from the mobility is straightforward for systems that fit the Smoluchowski model, i.e. particles larger than about 0.2 microns dispersed in electrolytes containing more that 10-3 molar salt.
|
For small particles in low dielectric constant media (eg non-aqueous media), f(ka) becomes 1.0 and allows an equally simple calculation. This is referred to as the Huckel approximation.
The essence of a classical micro-electrophoresis system is a capillary cell with electrodes at either end to which a potential is applied. Particles move towards the electrode, their velocity is measured and expressed in unit field strength as their mobility.
Early methods involved the process of directly observing individual particles using ultra-microscope techniques and manually tracking their progress over a measured distance. This procedure, although still being used by many groups worldwide, suffers from several disadvantages, not least that of the strenuous effort required to make a measurement, particularly with small or poorly scattering particles. The technique used in Malvern Panalytical's Zetasizer Nano range of instruments is laser Doppler electrophoresis in combination with M3-PALS.
The Zetasizer Nano Series uses a combination of laser Doppler velocimetry and phase analysis light scattering (PALS) in a patented technique called M3-PALS to measure particle electrophoretic mobility. Implementation of M3-PALS enables even samples of very low mobility to be analyzed and their mobility distributions calculated.
PALS can give an increase in performance of greater than 100 times that associated with standard measurement techniques. This allows the measurement of high conductivity samples, plus the ability to accurately measure samples that have low particle mobilities, such as samples dispersed in non-aqueous solvents. Low applied voltages can now be used to avoid any risk of sample effects due to Joule heating.
Further information discussing the techniques of laser Doppler electrophoresis and M3-PALS can be found in various articles available on the Malvern Panalytical website.
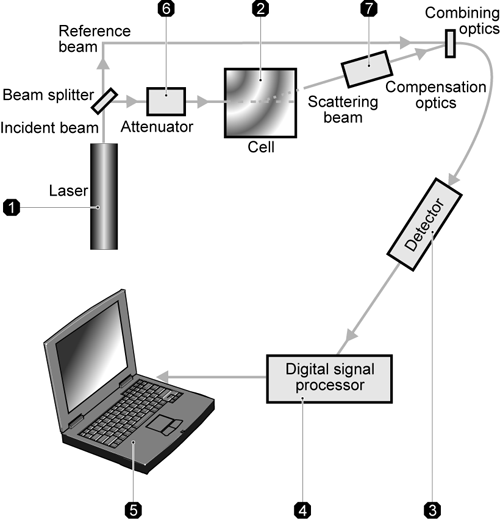
A zeta potential measurement system comprises of six main components (figure 10). Firstly, a laser is used to provides a light source to illuminate the particles within the sample. For zeta potential measurements, this light source is split to provide an incident and reference beam. The incident laser beam passes through the center of the sample cell, and the scattered light at an angle of about 13o is detected. When an electric field is applied to the cell, any particles moving through the measurement volume will cause the intensity of light detected to fluctuate with a frequency proportional to the particle speed and this information is passed to a digital signal processor and then to a computer. The Zetasizer Nano software produces a frequency spectrum from which the electrophoretic mobility and hence zeta potential is calculated. The intensity of the detected, scattered light must be within a specific range for the detector to successfully measure it. This is achieved using an attenuator, which adjusts the intensity of the light reaching the sample and hence the intensity of the scattering. To correct for any differences in the cell wall thickness and dispersant refraction, compensation optics are installed to maintain optimum alignment.
|