粒度分析的基本原理-1
粒度分析的基本原理
什么是颗粒?
这个问题看起来非常愚蠢,但在各种粒度分析技术中,这是一个基础问题。分散过程和材料的形状在粒度分析中从一开始就更复杂。

粒径问题
假设你给别人一个火柴盒,让他们说出这个火柴盒的尺寸。人们可能会回答这个火柴盒的尺寸是20*10*5mm。你不能准确地说“火柴盒的尺寸是20mm”,对于复杂形状如沙粒或颜料罐中的色素颗粒来说,这是一个更大的挑战。如果我是质量管理经理,我想要用一个数值来描述颗粒,例如想知道最近生产的产品的平均尺寸是增加还是减少了。这是粒度分析中的基本问题——我们如何能用一个数值来描述一个三维物体?
等效球体
有一种球可以用一个数字来表示。如果我们说一个直径为50μm的球,那它可以准确地表示。但当我们谈到50μm的立方体的棱角和对角线,就无法精确表达。很多有复杂特征的物体可以用一个数来表示。例如,关于体积和表面积的重量是一个特定的数值。所以如果有一种技术可以测量火柴盒的重量,我们可以将其转换为等效球的重量。
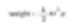
记住要计算一个和火柴盒重量相同的球的直径(2r)。这就是等效球理论。我们测量颗粒的特性并假设它们是球状颗粒。因此,得到一个用于表示颗粒的特定数值(球的直径)。
当描述三维物体时,这种方法虽然在控制目的上没有更精确的方法方便,但不需要用3个或更多数值来表示。
我们可以看到这对物体形状的影响是有趣的,并以球状的圆柱体为例。

但如果圆柱体的形状或尺寸发生变化,体积/重量将不同。作为等效球模型,我们至少可以说它变小或变大了。
100 x 20μm 圆柱体的等效球形直径
设想一个圆柱体的直径D1=20μm,高度为100μm。有一个与圆柱体等体积的球,其直径为D2。我们可以通过以下公式计算直径。
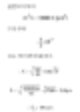
高度100μm,直径20μm的圆柱体的球形直径大约是40μm。下表展示了各种比例的圆柱体的球形直径。最后一行是典型的盘状大颗粒,例如粘土颗粒。由于其高20μm,厚度仅0.2μm,通常不会考虑其尺寸。对测量粒子体积的工具来说,我们可能得到大约5μm的答案。因此对于这种回答提出异议的可能性,需要使用其他技术。
这些圆柱体还可以表现为和25μm滤纸一样的尺寸,这时可以说“所有物质都小于25μm”。这些圆柱体由于不同的值,在激光衍射时会表现出不同的结果。

各种测量技术
显然,如果透过显微镜观察颗粒,可以看到它们以二维投影的方式存在,其中的特征可用于测量和描述颗粒的直径。如果我们选择颗粒的最大长轴作为尺寸,便可以说该颗粒是具有最大维度的球状颗粒。类似的,如果使用最小直径或Feter’s直径这样的量度,我们将得到颗粒尺寸的另一种解答。因此,我们必须了解不同技术可以测量颗粒的不同物性(最大长轴、最小长轴、体积、表面积等)。选择不同的测量技术会导致不同的结果。

Figure 3显示了用于描述单颗砂粒的多种解答。每种技术都没有错 – 每种方法都可以测量颗粒的不同性质。就像用厘米或者英寸来测量火柴盒(你量长度而我量宽度!)。
因此,我们只能用相同的测量技术对粉末状材料进行测量并进行比较。这意味着像砂粒这样的颗粒没有标准尺寸。必须通过各技术之间的比较来定义标准。然而,通过每种技术,我们可以获得标准粒度尺寸,并比较应用该技术的设备。
D[4,3]等
假设有三个球,其尺寸为1、2、3单位。三个颗粒之间的平均尺寸是多少?最开始我们可能会说是2。那我们是怎么得到这个答案的呢?我们把所有值加起来,再除以总颗粒数。
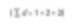
这是数值平均(更准确地说是长度平均数)。颗粒的数目可以通过公式来表示。

数学术语中称为D[1,0]。这是因为公式上面的直径项为(d1)并且公式下面没有直径项(d0)。但假如我是催化剂相关的工程师,我可能希望根据表面积来比较这些球。因为更高的表面积能获得更高的催化效率。球的表面积为4πr2。因此以表面积为基础进行比较时,必须计算直径的平方和,然后除以颗粒数,并取平方根来获得平均直径。

这同样是数值平均(基于表面积的平均)。原因是颗粒个数出现在公式中。我们将所有直径的平方相加。因此数学术语中称为D[2,0]。 – 公式的上面平方直径,下面没有直径。假如我是化学专业的,我可能希望基本的重量能比较球。球的重量由以下公式决定。
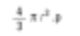
然后除以粒子的数目并取立方根以获得平均直径。

再次,这是数值平均(数-体积或数-重量平均)。原因是颗粒个数出现在公式中。数学上称为D[3,0]。
D[1,0],D[2,0],D[3,0] 简单平均的问题在于颗粒个数对公式的特定性。这需要计算大量的颗粒数。通常只有在较低的数量(ppm或ppb)情况下,在应用比如污染、控制和清洁时实行。一个简单计算表明,如果1克硅(密度2.5)的尺寸全部是1μm,则大约有760*109颗粒。
因此必须要补充瞬时平均的概念,这可能会导致困惑。以下是两个重要的平均值。
-
D[3,2]- 表面积平均 – Sauter平均直径
-
D[4,3]- 体积或质量平均 – De Brouckere平均直径
这些平均值与惯性矩相似,并引入了与另一直径有关的线性术语。(例如,表面积与d3成比例,体积和质量与d4成比例。)
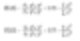
这些公式显示了频率(表面积或体积/质量)分布的中心循环。实际上,它们是每个分布的重心。这种计算京法的优点显而易见 – 公式不包含颗粒个数,因此计算平均值和分布时并不需要复杂的颗粒数知识。激光衍射首先基于体积项进行贡献计算。这就是为什么D[4,3]被标明为清晰的测量方法。
不同的测量技术会导致不同的结果
假设我们使用有栅格的电子显微镜来测量颗粒的直径,将颗粒的直径全部加上再除以颗粒数以得到平均结果。我们这个例子展示这 …
这篇文章可能已被自动翻译
{{ product.product_name }}
{{ product.product_strapline }}
{{ product.product_lede }}
