입도분석의 기본원리-2

下载



数分布和体积分布 

 

  上述示例来自 New Scientist (1991 年 10 月 31 日)，显示了在宇宙中围绕地球的轨道，以及它们的规律性轨道目的的大数。科学家还根据它们的大小进行分类。如果我们检查上述第三段，我们可以推断出所有颗粒中的 99.3% 都惊人地小。这是对基于数字的数据进行评估。但如果我们检查第四段，实际上我们可以推断出所有物体在 10-1000cm 之间。这是所有物体的质量。数量和质量的分布非常不同，我们必须注意，根据我们使用的分布，结论可能会有所不同。同时，没有任何分布是完全准确的。数据仅以不同方式检查。例如，如果我们制造宇航服，可能会说必须避免 7000 的大物体，并对 99.96% 的情况保持警惕。但在宇航服中，最重要的是保护那些占数字 99.3% 的小颗粒。如果我们计算图表中分布的平均值，那么我们需要知道数的平均值约为 1.6cm，重量平均约为 500cm。差异会如此之大。

数，长度，体积/质量分布的转换

  如果通过电子显微镜测量颗粒，那么根据前面的内容（不同的技术提供不同的平均值），我们会计算 D[1,0] 或数-长度的平均大小。如果我们真正需要的是质量或体积的平均大小，则需要将数平均值转换为质量平均值。从数学上来说，这很容易实现，但我们需要测量这种转换结果的影响。

  假设电子测量技术对平均大小的误差为+-3%。当我们将数平均大小转换为质量平均大小时，质量平均值会以直径的立方体函数表示，那么误差会是最后值的立方值或+-27%。 

 











  但是，如果通过激光散射计算质量或体积分布，情况会有所不同。

  在溶液分散法的循环条件下测量稳定样品时，可以产生+- 0.5%的重复使用体积平均值。

  如果现在将此体积平均值转换为数平均值，那么误差或数平均值将是 0.5% 的立方根，甚至不到 1.0%。

  实际上，这意味着如果我们使用电子显微镜来获取体积或质量分布，失去一个 10μ 的颗粒，相当于失去 1000 个 1μ 的颗粒。因此，我们必须意识到这种互转换的巨大风险。

  Malvern Sizers 中的 Dos 和 Windows 软件都将计算不同直径。但我们在找到这些直径时必须非常小心。各种不同的方式（即方法）通过接下来的公式（Hatch-Choate 转换公式-Ref.7）互相转换。

 

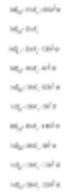
测量和导出直径

  我们已经看到 Malvern 激光衍射技术提供了用于分析光能数据的体积分布（注意到根据 Fraunhofer 分析，假定了面积分布）。该体积分布可以如上所示转换为任何数或直径。

  然而，在任何分析技术中，我们需要了解这些转换结果以及结果的影响。实际上，平均直径是由机器实际测量的，而某些直径是通过计算或第一次测量到的直径得出的。

  不同的技术将能够从一些已经测量的直径中推导出其他直径。例如，显微镜将测量 D[1,0]，并从中得出其他直径。

  我们可以更加信任测量的直径，而不是推导出的直径。实际上，在某些实例中，依赖于推导（计算）特性可能相当危险。例如，Malvern 分析表会向我们展示特定表面积（m/cc 或 m/gm）。

  我们不应该完全接受所提供的信息。换言之，如果我们真心想获得一种材料的特定表面积，我们需要使用专门的技术（B.E.T 或水银孔径法）来进行计算。

用什么样的数？

  另一种已知技术是测量颗粒的其他属性（或大小），我们需要在不同的方法中使用数据来获取不同的平均值结果（如 D[4,3], D[3,2] 等）。那么我们为什么要使用数量呢？

  以直径为 1 和 10 单位的球为简单示例。假设我们在制造金。如果我们计算一个简单的数平均直径，这将如下面的公式描述。

 

 

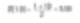
  因此，我们可以假设系统中颗粒的平均大小是 5.50 单位左右。然而，如果我们真的在制造金，我们必须记住，我们关心的是材料的重量。

  例如，如果我们了解过程的趋势，我们可能对其中 350 万颗粒没有兴趣。相反，我们对 1 公斤或 2 公斤的金属更感兴趣。

  记住质量平均值是直径的立方函数，我们知道直径为 1 单位的球有 1 单位的质量，直径为 10 单位的球有 10=1000 单位的质量。

  这意味着更大的球构成了系统总质量的 1000/1001 部分。如果我们在制造金，我们可以舍弃直径 1 单位的球，因为我们将失去的质量不到系统总质量的 0.1%。因此，数字平均不会在系统的质量中占据重要的部分。这在 D[4,3] 中更有用。

  在我们的两个球的示例中，质量或体积平均动量将如以下公式计算。

 

 

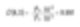
  这些数字展示了系统内质量的集中位置，对于化学过程工程师来说是有价值的。

  然而，假设我们在洁净室内制造硅或砷化镓晶圆。在这种情况下，如果有一个颗粒落在晶圆上，可能会导致缺陷。实际情况下，颗粒的数量或浓度非常重要。因为一个颗粒会造成一个缺陷，我们希望使用能够直接测量一定数量颗粒或颗粒浓度的技术。本质上，这与颗粒的总数和大小不同。总数的情况下，我们记录并计数每一个颗粒。大小不太重要。而我们只需要特定的数量规模即可（参考 8）。从大小观点看，特定大小的颗粒对大小和颗粒的大小贡献非常无关紧要。因此我们需要更多的大小范围。

  测量用于哮喘患者的一个剂量吸入器时，药物的量和颗粒大小的贡献都很重要。

平均、中位数、众数 – 基础统计 

 

平均 (Mean)

  这是任何数据的算术平均。有很多可以计算颗粒的平均数 (参见 D[4,3] 部分等)

中位数 (Median)

  这正好是将总体分成两半的颗粒大小的值。例如，上述值分布的 50% 与 以下的 50% 上下限。 

众数 (Mode)

  频率曲线的最高点即频率分布中的最常见值。假设这个分布是 Nomal 或 Gaussian 分布。平均值、中位数、众数正好处于同一位置。参见第 4 图。然而，假设这个分布如图 5 所示是双峰 (Bimodal) 的。

 

 

  平均直径将位于几乎正好位于两个分布之间的图中位置。值得注意的是，实际上没有这种中平均大小的颗粒。中位直径会接近更高的分布的 1%。因为这一点正好将其分成两个数据所况。众数将是更高的分布的峰值，因为这是最常见的直径值。



  数据对称性导致的平均值、中位数、众数没有理由必须是理想的甚至相同的，这个例子说明了这一点。