This white paper discusses the principals of enzyme kinetics and details experimental design and analysis of enzyme kinetics with ITC. Several case studies are presented.
Enzymes are proteins that function as biological catalysts and they play a crucial role in nearly all processes that take place in living organisms. Therefore studies of these molecules and the reactions they catalyze have been a core activity for biochemists for at least the past fifty years. Apart from the fundamental scientific interest, investigations into enzyme function are important in order to develop novel therapeutics against diseases such as cancer. A large group of drugs currently used in the clinic exert their primary biological effects by inhibiting a specific enzyme (1). Development of next generation inhibitors requires that we understand the way the enzyme binds and processes the natural substrate.
To understand any biochemical phenomena it is necessary to study the enzyme reactions which make up that system individually. The aim is to learn how and why the enzyme recognizes its substrate and the mechanism it employs in catalyzing the reaction to form the product. Modern techniques in molecular biology, sequencing, and proteomics have led to an upsurge in the number of enzymes that can be routinely expressed as recombinant proteins. Substrates or substrate analogues can also be produced using the same technology or chemically synthesized. Once the two components have been obtained it is then necessary to develop an assay technique that allows the enzyme-catalyzed reaction to be studied. When these data are combined with structural studies a picture of the enzyme mechanism can emerge that allows potential inhibitors to be developed based on a rational approach.
Development of suitable assays is often problematic; some of these difficulties are discussed below. In an effort to address these problems high-sensitivity ITC has been successfully applied to quantitatively monitoring enzymatic reactions in order to obtain the associated Michaelis-Menten kinetic constants that describe the system. ITC is a well established, powerful and versatile technique that is widely used for measuring the thermodynamics of equilibrium association reactions (2-6). The technique directly and model independently measures the change in binding enthalpy (∆HB) for reversible interactions. In addition, well designed experiments can yield an approximate value for the equilibrium association constant (KA) for the enzyme-substrate complex when product formation is the limiting step, as well as the stoichiometry (n) of the reaction. Therefore ITC can yield an almost complete thermodynamic profile for any bimolecular complex formation.
In this white paper the application of ITC for examining catalytic reactions will be explored. We are interested in mechanistic studies of two classes of enzyme (phosphatases and Ap4A hydrolases). The results of previous work on these enzymes involving ITC will be discussed from a practical viewpoint. These data will also be used to demonstrate how ITC-derived enzymatic reaction data can be analyzed in order to obtain enzyme kinetic parameters.
Current theories to explain enzyme-substrate interactions revolve around the induced fit model. Here the initial interaction is quite weak, however these weak interactions rapidly induce conformational changes in the protein that strengthen binding and bring catalytic active sites in close proximity to substrate molecules. After the initial binding event, one or more mechanisms of catalysis generates transition-state complexes and reaction products. Some possible mechanisms of catalysis include induced bond strain in the substrate, orientation of reactive groups to place them in close proximity with one another, the use of proton donors (acids) and acceptors (bases), and covalent mechanisms involving covalent intermediates.
When an enzyme interacts with its substrate(s) it forms an enzyme-substrate complex (ES). This complex then gets converted to the transition state (ES*); and the transition state complex is then transformed into an enzyme-product complex (EP), which finally dissociates to give product and free enzyme. In biological systems where the concentration of substrate is much higher than that of the enzyme these steps can be simplified and summarized as:
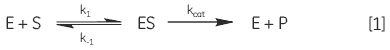
|
where E is enzyme, S is substrate, ES is enzyme-substrate complex, P is product, k1 is the rate constant for the formation of ES, k-1 is the rate constant for dissociation of ES back into E + S, and kcat is the catalytic rate constant. The kinetics of simple reactions of this type were first analyzed by Michaelis and Menten in their classic paper of 1913 (7). Their approach to analyzing enzyme-substrate kinetics is still the principal method by which enzymes are characterized today. The Michaelis-Menten equation is given below:

|
where v is the rate of an enzyme catalyzed reaction, Vmax is the maximal velocity that would be observed when all the enzyme is present as ES, [S] is concentration of substrate and KM is the Michaelis constant. It is derived from the three rate constants shown in Equation 1 [KM = (k-1 + kcat)/k1] and it can be approximately considered as a measure of affinity of binding between the enzyme and its substrate when product formation is the rate limiting step. The lower the KM the greater the affinity, that is the lower the concentration of substrate required to achieve a given rate. Also since Vmax = kcat [E]totalthe above equation can also be written as:

|
Equations 2 and 3 are a quantitative description of the relationship between the rate of an enzyme catalyzed reaction, the concentration of substrate and two constants: Vmax and KM. These relationships can be used to demonstrate that at the substrate concentration where exactly half of the maximum reaction rate, (i.e., ½Vmax), can be achieved, is numerically equal to KM. This fact provides a simple yet powerful bioanalytical tool that has been used to characterize both normal and altered enzymes. The Michaelis-Menten equation has the same form as the equation for a rectangular hyperbola; graphical analysis of reaction rate (v) versus substrate concentration [S] produces a hyperbolic rate plot. Figure 1 shows an example of such a curve.
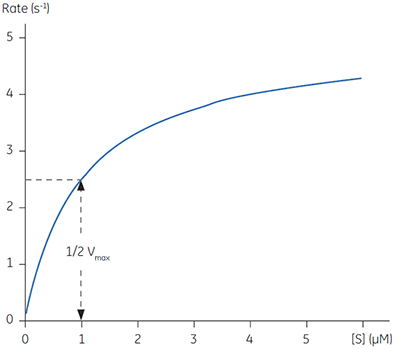
|
In principle experimentally determining the Michaelis-Menten constant and Vmax is quite simple. A series of different substrate concentrations are prepared, at time zero a fixed amount of enzyme is added and over the next few minutes the concentration of product formed is monitored. Typically such methods rely on either the substrate or product absorbing light at wavelengths amenable to spectrophotometers. Early in the assay, when the amount of substrate is in excess over the enzyme, the observed rate is linear with time and is referred to as the initial velocity (Vi). Plotting initial velocity vs substrate concentration allows a plot similar to that shown in Figure 1 to be constructed. In situations where the product does not have a convenient chromophore significant problems can arise. Even if one particular product can be monitored spectroscopically it is almost certainly the case that substrate analogues may not have such features. Clearly when designing substrate analogues in order to probe enzyme mechanism one should only have to consider the chemistry of the catalytic reaction rather than issues around performing assays. The latter can often complicate design strategies since the inclusion of a chromophore can be cumbersome and expensive.
Alternative methods involve mixing enzyme and substrate using stopped flow or quench flow techniques. Here the reaction is allowed to proceed for differing time scales before being quenched using, for example, a pH jump for example. The reaction intermediates can be collected at given time periods and the amount of formed product quantified using mass spectrometry or chromatography. These are specialized techniques that are often very useful for measuring fast kinetics or isolating intermediates. However, for routine analysis these methods can be time consuming and expensive. In this context ITC is a generally applicable assay technique that can be ubiquitously applied to almost any enzyme catalyzed reaction as long as there is a heat signal associated with the reaction. The experiments are quick (typically ~2 hours) and use small amounts of material.
In order to measure enzyme kinetics it is necessary that an observable event accompany the transformation of substrate into product. ITC can be used to measure enzyme kinetic parameters because the thermal power generated as the reaction proceeds is a direct and sensitive observable event. The use of ITC to measure the heat generated during an enzymatic reaction is well established (8-13). The rate of a reaction is directly proportional to the thermal power, defined as the heat (Q) produced as a function of time (dt): Power = dQ/dt. The minimum response time of MicroCal VP-ITC is about 15 seconds and therefore the enzyme reaction rate of many processes are slow enough to be studied with this instrument; this means that the observable thermal power need not be corrected for the time constant of the calorimeter (13). By using the normal titration mode of the ITC, multiple injections of substrate can be made providing multiple rate determinations under steady-state conditions within a single experiment. Furthermore, the high-sensitivity of modern ITC instruments means the amounts of enzyme required are often similar to those used in spectrophotometric assays, but generally higher than the amount required in radioactivity assays.
The theoretical basis of using ITC for determining enzymatic rate kinetics has been outlined in three excellent papers (10,11,13). These authors have shown that the amount of heat involved with converting n moles of substrate to product is given by the following expression:

|
where ∆Happ is the total molar enthalpy for the reaction, determined experimentally, P the concentration of product generated and V is the volume of the reaction solution, that is the cell volume. It can be easily seen from Equation 4 that measuring the thermal power generated by the enzyme as it catalyzes conversion of substrate gives a measure of the reaction rate since:
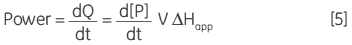
|
where d[P]/dt is equal to the rate of product formation, that is the rate of reaction, therefore Equation 5 can be rearranged to give:
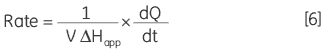
|
From Equation 6 it is clear that in order to obtain a Michaelis-Menten plot it is necessary to use the calorimeter to measure two parameters: 1) The total molar enthalpy must be determined in experiments where there is sufficient enzyme in the cell to convert all the injected substrate into product in a given time period. These experiments give rise to peaks where the baseline response returns to the same value after the substrate injection as it was before the injection. Integration of these peaks with respect to time yields the total heat produced by the reaction and dividing this total heat by the amount of substrate converted gives the total enthalpy change. 2) The power generated (dQ/dt) must be determined at different substrate concentrations. How this is achieved is illustrated using some real examples below.
An alternative strategy for obtaining enzyme kinetic parameters involves continuous rate measurements after a single injection of substrate at concentrations higher than KM. In these experiments thermal power is monitored as the substrate is completely depleted. At any given time the reaction rate can be determined using Equation 6 and the concentration of substrate at any given time can be determined from the integral of the heat evolved. Therefore plots of rate vs substrate concentration can be plotted to give a continuous kinetic curve.
A major advantage of using calorimetry to study enzyme catalyzed reactions is that Michaelis-Menten based kinetic and thermodynamic data can be obtained simultaneously. Specifically, determining values for KM can be useful for several reasons: 1) Knowledge of the KM establishes approximate concentrations of intracellular substrate; 2) The KM is constant for a given enzyme, therefore this parameter provides a convenient way of comparing isoforms of an enzyme from different organisms or tissues; 3) Enzyme activity can be modulated by ligands and ligand induced changes in KM can be used to identify important inhibitors.
In addition, direct measurement of apparent molar enthalpy for the reaction under study provides an insight into the energetics of the system and allows the overall free energy to be dissected into component enthalpic and entropic terms. For a reaction that involves the release or uptake of protons during catalysis, the calorimetrically determined enthalpy is sensitive to the buffer ionization enthalpy (∆Hion). The apparent observed molar enthalpy for the reaction is made up of an intrinsic enthalpy for the enzymatic reaction (∆Hion) as well as an ionization enthalpy for each proton released or absorbed by the buffer (∆Hion):
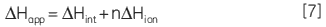
|
where n is the number of protons released or absorbed by the buffer. This relationship can be easily investigated by simply measuring ∆Happ at a fixed pH but using different buffers, each with a known ∆Hion. A resultant plot of ∆Happ vs ∆Hion should yield a straight line in which the slope is equal to n and the intercept is equal to ∆Hint. Therefore ITC has the potential to provide detailed enzyme-substrate rate kinetic and energetic insights into enzyme-catalyzed reactions, especially where linked protonation effects are important.
In order to thoroughly investigate an enzyme system, important factors that must be examined are enzyme concentration, ligand concentrations (substrates, products, inhibitors and activators), pH, ionic strength and temperature. When all of these factors are studied and analyzed correctly it is possible to understand the nature of an enzyme catalyzed reaction in great depth. For example, by varying the substrate and product concentrations it is possible to derive the order in which substrates add and products leave the reaction scheme, that is the reaction mechanism. By examining the effect of pH and temperature on the enzyme kinetic constants, the identity of amino acid side-groups involved in catalysis can be determined. ITC is a powerful and convenient experimental tool that allows all of the enzyme above experimental conditions to be manipulated in order to carry out a systematic characterization of an enzyme system in a label-free environment, bringing with it some economical benefits.
The first thing to note is that as with all ITC experiments it is important that the reactants are made up in appropriate and well defined buffer systems. In order to avoid excessive heats of dilution it is necessary to dialyse the enzyme in the chosen buffer and then use the same buffer to make up the substrate solution. Of course if practical the substrate can also be dialyzed in the same buffer. When choosing a buffer system, it is worthwhile remembering that it might be necessary to prepare substrate solutions at quite high concentrations. For example, we have examined the hydrolysis of ATP by ATPase, the substrate, ATP, was prepared to a concentration of ~35 mM and it was therefore necessary to ensure the concentration of buffer salt was much higher than this to ensure good buffering of the solution and prevent pH drift. As an added precaution it is prudent to check the pH of all solutions and mixtures both before and after performing titrations.
In order to measure ITC enzymatic assays with ITC it is necessary to accurately quantify the molar concentration of both enzyme and substrate. This is most conveniently done using spectroscopic means where the reactants have chromophores and experimentally determined or calculated molar extinction coefficients. Enzymologists often like to express amounts of protein in terms of activity units, where 1 unit of an enzyme is defined as that amount that catalyzes the formation of 1 µM of product per minute under defined conditions. If an enzyme preparation is impure the concentration may be expressed as units per ml. The specific activity is defined as units per mg of protein; the greater the purity of the preparation, the greater the specific activity. With ITC, it is necessary to determine the apparent molar enthalpy, making it advantageous if the exact molar concentration of active enzyme can be determined in the solution. It is also helpful if there is some indication of approximate KM so that appropriate substrate concentrations can be used to yield a complete Michaelis-Menten curve with some points of the curve below KM and some above it. Therefore it also becomes necessary to accurately determine substrate concentrations in solutions.
To actually perform the ITC assay, two types of experiments need to be carried out. Firstly, the total molar enthalpy can be determined by having relatively high concentrations of enzyme in the cell, relatively low amounts of substrate in the injection syringe, and by leaving sufficient gaps between injections to ensure that all of the substrate is converted to product. The resultant peaks can be used to obtain ∆Happ in the normal way. Secondly, rate data can be obtained by having relatively low amounts of enzyme in the cell, relatively high amounts of substrate in the injection syringe and by leaving shorter gaps between injections. The aim here is to ensure that subsequent to each injection, steady-state conditions are maintained and no more than 5% of the substrate is depleted prior to the next injection. These two sets of data are sufficient to derive the Michaelis-Menten defined enzyme parameters KM, kcat and Vmax. In addition, it is also necessary to perform the usual dilution experiments where the identical solutions of substrate used in enzyme assays are injected into the reaction buffer alone. Examples of this type of data and the analysis required to obtain enzyme kinetic constants are illustrated below using two enzyme systems under study in our laboratories.
Reversible protein phosphorylation is a critical process through which cellular function is controlled. The fine balance of phosphorylation states is achieved by the competing actions of kinases and phosphatases. If this balance is upset a wide range of disease states can result. In this study we present enzyme rate data for a serine/threonine phosphatase (PP1-γ, see Fig 2). This enzyme catalyzes the direct attack of water and it requires metal ions for activity. Due to the ubiquity of these enzymes and an appreciation of their potential as therapeutic targets the mechanism and control of phosphatases has been the subject of intense biochemical and structural study. However a clear mechanistic understanding of their catalytic action has not been achieved. We are currently employing ITC to examine this system in detail. As a prerequisite it was necessary to establish that ITC could reproduce data on a substrate for this enzyme commonly used in spectrophotometric assays. It was necessary to validate ITC for enzyme assays in our system using a known enzyme-substrate complex before analyzing novel substrates. In the present study, we used PNPP as a model substrate to directly compare spectrophotometrically and calorimetrically determined enzymatic rate parameters.
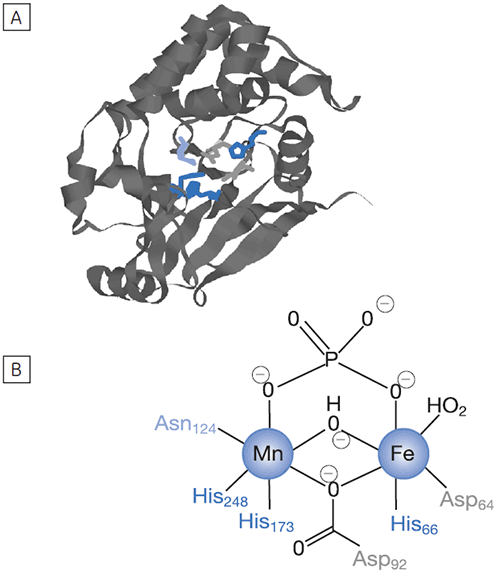
|
Using the enzyme shown in Figure 2 and PNPP as substrate, we performed the two types of ITC experiment highlighted in the preceding section. Figure 3 shows the results of an assay designed to obtain rate data for this catalytic reaction.
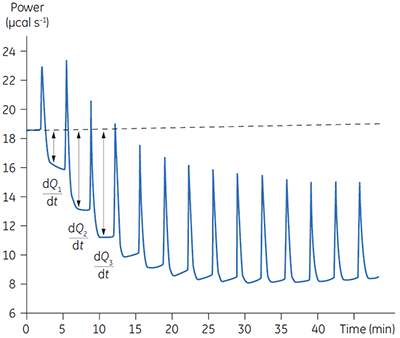
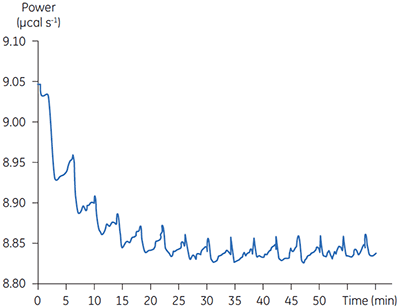
Fig 3. Raw calorimetric data for the measurement of the reaction rate for the hydrolysis of PNPP by PP1-γ. The dashed line is a linear least squares best fit to the preinjection baseline.
|
After initial equilibration, a 2 µl injection of 100 mM PNPP was made into the calorimeter cell containing a 0.68 µM dilution of enzyme. This resulted in an initial endothermic peak corresponding to the heat of dilution. The baseline then stabilized at a lower power level than the preinjection value. This is because some heat is generated by the enzymatic reaction and therefore correspondingly less power is supplied by the instrument in order to maintain thermal equilibrium. The drop in baseline also indicates that this particular reaction proceeds with a negative (exothermic) enthalpy. A second injection is made three minutes later and the process is repeated. The rate of heat generated (power: dQn/dt) at each substrate concentration is proportional to the rate of reaction.
Knowing the substrate concentration and the volume of the calorimeter cell as well as the injection volume, it is possible to calculate the substrate concentration in the cell after each injection. It is then necessary to determine the value of dQ/dt, that is the drop in baseline power level, at each substrate concentration. In practice it is often the case that the preinjection baseline is not completely horizontal. In such circumstances, it is valid to fit a line of linear best fit to a portion of the pre-injection baseline and use this line to make estimates of dQ/dt. Similarly there may not be a flat baseline following the injection; again a best fit straight line can be used for a 30-second period immediately before the next injection. Of course, in the period between injections, steady-state conditions should prevail. Values of rate determined in this way will yield data in units of µcal per second. These can be readily converted to turnover in units of sec-1 by dividing by ∆Happ, protein concentration and volume. It is also necessary to take into account the slight dilution of protein in the cell that takes place upon injection of substrate. The data shown in Figure 3 were initially analyzed using a Microsoft™ Excel™ spreadsheet.* Fitting of rate data was performed using the non-linear least squares analysis package in Origin™ 5.0.
As alluded to above, ∆Happ was measured separately. Figure 4 shows the results of such an experiment for the PP1-γ-PNPP system.
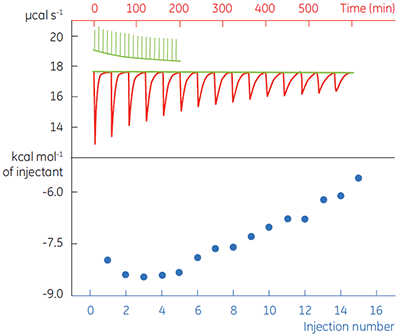
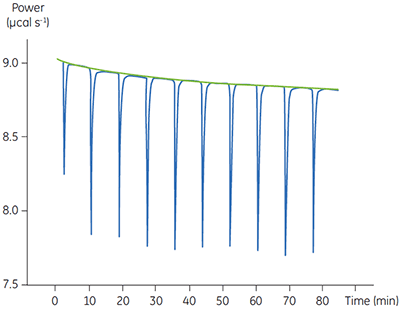
Fig 4. In the top panel the red peaks are raw calorimetric data for the determination of ∆Happ for the hydrolysis of PNPP by PP1-γ. Integration of these peaks gives the data in the bottom panel. Heats of substrate dilution are shown in green in the upper panel.
|
In the top panel of Figure 4, the red line shows the heats produced when 15 injections of 2 µl 100 mM PNPP was injected into buffered enzyme in the cell at a concentration of 13.6 µM. A forty-minute gap was left between each injection to ensure the baseline returned to the initial value, indicating that all the substrate had been used up. The green line in the top panel shows the heats of substrate dilution. Integration of the peaks in the upper panel with respect to time allows ∆Happ for each injection to be determined (lower panel). A key feature of this data is that the magnitude of ∆Happ decreases after each injection subsequent to the fifth injection of substrate. This effect is due to product inhibition. In this reaction the product is inorganic phosphate, which inhibits PP1-γ with a Ki of about 1.6 ± 0.9 mM. This is consistent with the level of inhibition observed in Figure 4. For the purposes of data analysis, we ignored the first injection and took the average of the next four injections, that is up to a point where the concentration of Pi was too low to cause any significant inhibition. This gave a value for ∆Happ of -8.72 ± 0.35 kcal mol-1. This experiment highlights the importance of checking for product inhibition. This can be achieved by ensuring a large number of injections are made in experiments of this type. This approach is also advantageous since each injection represents an independent determination of ∆Happ and therefore a statistically meaningful value for this parameter can be obtained.
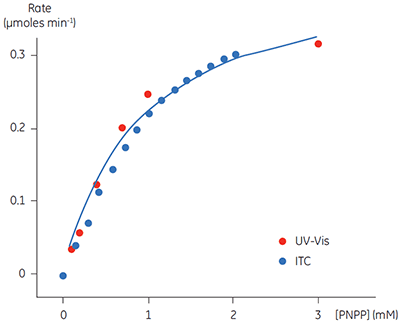
A key goal in this study was to evaluate ITC for use in kinetic assays for this enzyme system, and compare enzymatic parameters determined from ITC to those from other assays. This is why PNPP was chosen as a model substrate since a well established spectroscopic assay exists for this compound. In order to assess our calorimetric data we performed spectroscopic assays in an analogous way to the assays performed using ITC. The spectroscopic assay was used to determine initial velocities at a range of substrate concentrations for construction of a Michaelis-Menten plot. Combined ITC and spectroscopic data are shown in Figure 5.
Fig 5. Rate vs substrate concentration data for the hydrolysis of PNPP by PP1-γ. Two sets of data are shown (normalized for enzyme concentration), firstly rate data from ITC experiments (blue) and secondly the analogous data from spectrophotometric assays (red). The blue line is a non-linear least squares best fit to the spectroscopic data. The fitting was carried out in Origin 5.0 using Equation 3.
|
For the UV and ITC experiments, different concentrations of enzyme have been used, however to compare data, the results in Figure 5 have been normalized to the enzyme concentration used in spectroscopic assays. This can be easily achieved since Vmax is not a constant, but rather it is dependent on kcat, which is constant, and the concentration of the enzyme used in the assay, (Vmax = kcat [E]total). Therefore having determined kcat, Vmax for any given enzyme concentration can be calculated. For the ITC data the following values were obtained: KM = 1.2 ± 0.2 mM; kcat = 0.6 ± 0.1 s-1; Vmax = 0.43 mM min-1. The corresponding data from the UV assay were: KM = 0.9 ± 0.2 mM; kcat = 0.5 ± 0.1 s-1; Vmax = 0.39 mM min-1. Clearly, the enzymatic rate parameters obtained using two different techniques are in excellent agreement. These data are also consistent with earlier attempts to compare ITC and established spectroscopic assays (10). These experiments demonstrate that ITC can be reliably used to monitor reactions of this type routinely and accurately with substrates that do not possess any spectroscopic probes.
Dinucleoside polyphosphates (NpnN’s) are regulatory molecules that link the rate of protein synthesis to other essential processes such as DNA replication. The intracellular level of NpnN’s is determined by both their rates of synthesis and degradation.
|
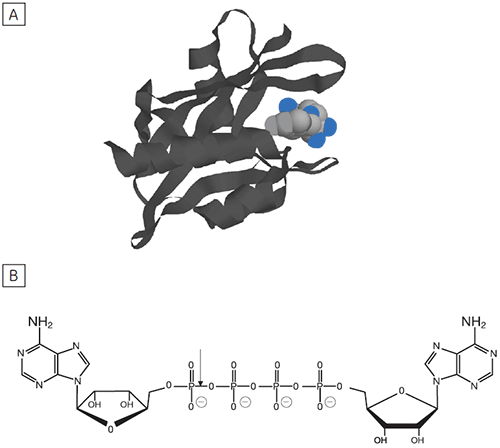
The principal enzyme responsible for the cleavage of Ap4A to ATP + AMP is Ap4A hydrolase, see Figure 6. Enzyme rate assays were carried out by ITC on Ap4A hydrolase using the tetraphosphate compound shown in Figure 6 as well as a similar pentaphosphate (Ap5A) compound. These experiments were carried out using the same procedure described for PP1-γ protein to obtain raw calorimetric rate data (Fig 7).
|
In these experiments, 2 µl injections of 1 mM P1,P4-di(adenosine-5’) tetraphosphate were delivered into the calorimeter cell containing 2 nM enzyme. The data were analyzed in the same way as described in the previous section. As before, enthalpy measurements were made in a separate experiment. These data are shown in Figure 8.
|
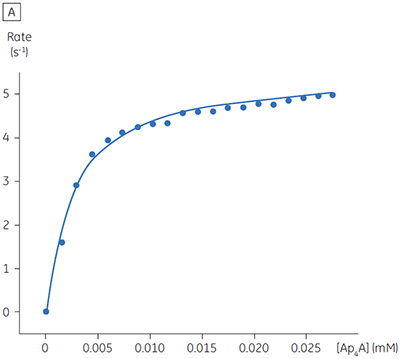
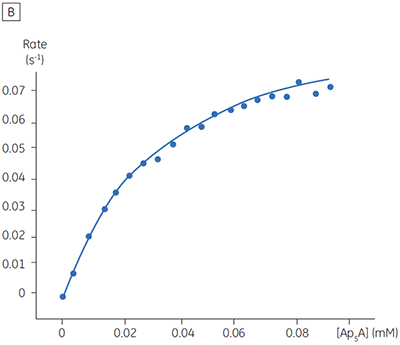
The blue line in Figure 8 corresponds to the heats produced from 10 consecutive injections of 2 µl 1 mM P1,P4-di(adenosine-5’) tetraphosphate (Ap4A) were made into buffered enzyme in the cell at a concentration of 100 nM. Sufficient time was left between each injection to ensure the baseline returned to the initial value (indicating that all the substrate had been used up). Integration of the peaks with respect to time allows ∆Happ for each injection to be determined. Unlike the situation with PP1-γ, no evidence for product inhibition was found and ∆Happ from nine independent determinations was measured to -19.24 ± 0.27 kcal mol-1. Similar experiments were performed with P1,P5-di(adenosine-5’) pentaphosphate (Ap5A) as substrate, with the resultant Michaelis-Menten plots shown in Figure 9; the kinetic parameters are summarized in Table 1.
| Substrate | KM (µM) |
kcat (s-1) |
Vmax (nM s-1) |
∆Happ (kcal mol-1) |
|---|---|---|---|---|
| Ap4A | 2.68 ± 0.80 | 2.76 ± 0.03 | 5.52 | -19.24 ± 0.27 |
| Ap5A | 34.5 ± 1.8 | 0.05 ± 0.01 | 1.0 | -18.38 ± 0.74 |
| ATP | nd | nd | nd | -8.6 ± 0.2 |
|
|
The initial enzyme kinetic data obtained with the human Ap4A hydrolase allowed the design of novel substrate analogues that should yield information on the exact mechanism of catalysis employed by this enzyme. As expected the enzyme is more efficient at catalyzing the hydrolysis of Ap4A as compared to Ap5A. However, the two enthalpy values determined for these two reactions are very similar as would be expected, since similar types of bond are being cleaved. ITC is currently being used to study the linked protonation effects associated with the action of this enzyme.
In order to develop novel therapeutics targeted towards important enzymes in disease states it is vital that we understand the way an enzyme works in vivo. This principally involves an examination of the enzyme catalyzed conversion of a specific substrate to a product. By elucidating the enzyme reaction rates parameters associated with this catalytic event it is possible to shed light on the mechanism of the reaction. With this information it is possible to understand the molecular determinants that dictate substrate specificity as well as the structural requirements for catalysis. This is a minimal level of understanding that must be reached before suitable inhibitors can be designed, synthesized and tested for their potential therapeutic value. In order for the pharmaceutical industry and academic researchers to develop new inhibitors as drugs, it is necessary to first understand how natural substrates and their analogues are processed by a particular enzyme of interest.
In order for these goals to be achieved, it is self-evident that suitable experimental tools must be in place that allows accurate and rigorous analysis to be performed. Traditionally, enzymologists have relied upon spectrophotometric assays where the presence of a chromophore/fluorophore on either the substrate or product allows quantification of turnover rate. When the substrate/product are spectroscopically invisible and they cannot be derivatized, biochemists usually have to carry out meticulous and very careful time course experiments. Here the catalysis is allowed to proceed for different time periods after which the amount of formed product is determined using chromatographic, electrophoretic or mass spectrometric means. Clearly these methods can be difficult, requiring a high level of expertise, and can be expensive and slow.
It is now becoming increasingly apparent that high-sensitivity isothermal titration calorimetry (ITC) offers a general methodology that can be used to obtain Michaelis-Menten rate information on enzyme function. ITC is already a proven technology for gaining detailed thermodynamic insights into equilibrium binding phenomena, and therefore factors such as baseline stability, reproducibility and overall sensitivity are well established. Monitoring the rate of a reaction using changes in thermal power is nondestructive, direct and very sensitive. Therefore it is possible to use ITC to obtain such data since rates are determined directly. The sensitivity of the instrument is such that levels of noise are constant, typically less than 0.01 µcal per second, irrespective of the thermal power generated during the chemical reaction. The mechanized titration capability of MicroCal ITC instruments means that the calorimetric assay is a “one-pot” method. Therefore numerous injections of substrate can be made into one reaction cell, thus eliminating experimental error associated with the preparations of different samples. ITC also allows experimental conditions such as temperature, pH, and ionic strength to be easily modulated. Hence a complete and in-depth analysis of an enzyme-catalyzed reaction can be undertaken, using the same methodology, to reveal important insights into enzyme mechanisms. The ITC assay can accommodate opaque solutions that would be impossible to analyze using spectroscopy. This means that the most physiologically relevant or chemically interesting compounds can be studied without any consideration of whether or not the compound is spectroscopically active.
The calorimetric data presented in this study as well as that for other enzymes in the literature (10-13) show that ITC is a generally applicable and accurate tool for quantitative enzyme kinetics. Data for the same system obtained through normal spectroscopic assays and through calorimetry are in excellent agreement, thus ITC has an additional and important advantage over other techniques. In addition to obtaining quality enzymatic rate information, calorimetry provides a thermodynamic insight into the reaction. This aspect of the ITC assay promises to revolutionize the amount and quality of information for enzyme catalysis with the potential to add another dimension to our understanding of these vital processes. Finally, using ITC to examine the kinetics of catalytic reactions need not be limited to enzymes. This technology and method will also be of use to physical-organic chemists who are engaged in designing and synthesizing organic catalysts for use in industrial applications or for other processes such as stereospecific synthesis.
This white paper was authored by Dr Ihtshamul Haq, Centre for Chemical Biology, Krebs Institute of Biomolecular Science, University of Sheffield, UK. The PP1-γ protein was expressed and purified at Sheffield Chemistry by Drs N. Williams and P. Lee-Robichaud. The author is grateful to Dr Q. I. Sheikh for conducting spectroscopic assays on this protein. The Ap4A hydrolase was a kind gift from Professor A. G. McLennan at the University of Liverpool. This project is run in collaboration with Professor G. Michael Blackburn at Sheffield Chemistry. Calorimetric titrations were conducted by Ms Elaine Frary in the IH laboratory. The author is also very grateful to Dr M. J. Todd for supplying a very useful spreadsheet for data analysis. IH is an EPSRC Advanced Research Fellow.
Sandler, M. and Smith, J. H., eds., Design of Enzyme Inhibitors as Drugs Oxford University Press, New York (1994).
Wiseman, T. et al. Anal. Biochem. 179, 131-137 (1989).
Ladbury, J. E. Structure 3, 635-639 (1995).
Jelesarov, I. and Bosshard, H. R. J. Mol. Recognit. 12, 3-18 (1999).
Haq, I. et al. Meth. Enzymol. 323, 373-405 (2000).
Haq, I. et al. Meth. Enzymol. 340, 109-149 (2001).
Michaelis, L. and Menten, M. L. Biochemische Zeitschrift 49, 333 (1913).
Spink, C. and Wadso, I. Meth. Biochem. Anal. 23, 1-159 (1976).
Watt, G. D. Anal. Biochem. 187, 141-146 (1990).
Morin, P. E. and Freire, E. Biochemistry 30, 8494-8500 (1991).
Williams, B. A. and Toone, E. J. J. Org. Chem. 58, 3507-3510 (1993).
Lonhienne, T. et al. Biochim. et Biophys Acta 1545, 349-356 (2000).
Todd, M. J. and Gomez, J. Anal. Biochem. 296, 179-187 (2001).
Goldberg, J. et al. Nature 376, 745 (1995).
Bailey, S. et al. Structure 10, 589 (2002).