Using the Zetasizer Nano to study concentration dependent changes in protein size

Introduction

The Zetasizer Nano utilizes the technique of dynamic light scattering (DLS) to determine the size of particles and molecules.

The wide size range and high sensitivity of the instrument have made light scattering measurements available to a much larger audience than previously accessible. In most cases the data produced show values and trends in line with expected behavior. Under two special experimental situations deviations from expected behavior can occur. These two are discussed in this technical note.

Full Diffusion Coefficient Treatment

In dynamic light scattering intensity fluctuations are measured. These fluctuations are caused by the diffusion of the scattering objects. In standard DLS data analysis the fluctuation rate is then related to the diffusion coefficient.

Historically, the measurement of diffusion coefficient assumed that the particles were dispersed at 'infinite dilution' - and in reality this assumption was more or less true. If the particle can be considered unaffected by neighbors, its movement only hindered by the effect of the viscous drag of the (Newtonian) liquid in which it is suspended, then the familiar Stokes-Einstein equation

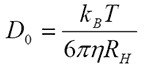
may be used to obtain the particle size. Here, the infinite dilution diffusion coefficient D₀ can simply be converted into a hydrodynamic radius R_H when the temperature T and the viscosity η are known (in addition to the Boltzmann constant k_B).

When particles are influenced by other neighboring particles, they are no longer freely diffusing and there are theories available that can help. A full treatment is beyond the scope of this technical note, yet it is useful to sketch the influence of interparticle interactions on the measured hydrodynamic size.

The function which describes the effect of neighboring particles is called the structure factor, typically denoted S(q) since it is dependent on the scattering vector q=2πnsin(θ/2).

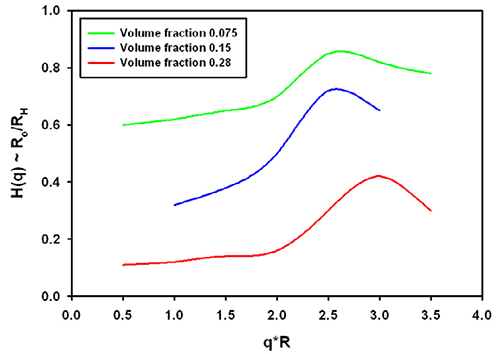
The function which describes the effect of the onset of diffusion, i.e. the movement before the collective viscosity of the liquid is experienced is called the hydrodynamic function typically denoted H(q), again dependent on the scattering vector.

It can be shown that the scattering vector dependent diffusion coefficient may be expressed as:

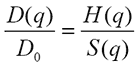
Using the inverse proportionality between the hydrodynamic size and the measured diffusion coefficient the above equation is equivalent to:

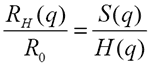
which means that the measured size at experimental conditions depends on the structure and the hydrodynamic factor and is NOT necessarily the same as the infinite dilution, 'ideal' size R₀.

Structure Factor

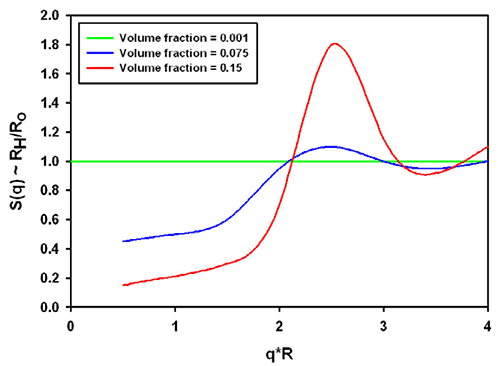
There is no analytical expression available for this factor*. However, experimentally obtained data [1] may be extrapolated to show typical values in figure 1. The clear message from the plot is that high concentration will reduce the measured hydrodynamic size. The influence can be quite significant, at 15% concentration this could result in an "under size" by more that 80%. This situation can happen, for example in pharmaceutical high protein concentration applications. The measured size could be a fraction of the expected size, when dealing with formulations at 100 g/L.

Figure 1: Structure factor versus scaled size. The measured size is shown at 0.1% v/v, 7.5% v/v and 15% v/v.

Hydrodynamic Factor

Again, no analytical expressions exist for this function. From the same reference discussed above [1], the H(q) is plotted in figure 2. The hydrodynamic factor has the opposite effect to the structure factor.

Figure 2: Hydrodynamic factor versus scaled size. At higher concentrations the effective size is increased.

Typically, the effective size could be increased if only hydrodynamics play a role. The exact contribution depends for example on the salt content of the buffer used in protein solutions.

Measured Effective Size

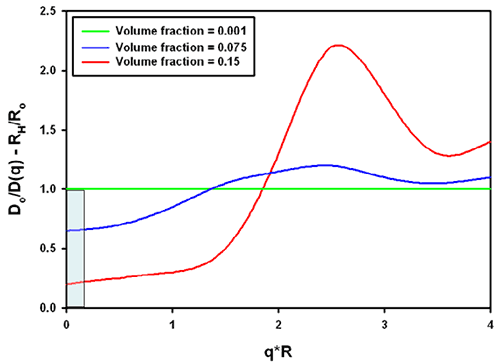
The combination of the structure and hydrodynamic factor leads to the effective measured size. From the same reference [1], data for charged colloidal particles are replotted in figure 3. The grey area was inserted to demonstrate the significance for typical protein molecules (which tend to be in a q*R range between 0.01 and 0.1 in a Zetasizer Nano with backscatter optics, a q*R of 1 is about 30nm radius). For charged particles at high concentration, the interparticle and hydrodynamic effects combine to lead effectively to a smaller size in all cases.

Figure 3: Effective size of charged colloidal spheres. For typical proteins (smaller than 10nm diameter in a Zetasizer Nano), the accessible region is highlighted with grey. For high concentration or low salt conditions the measured size will appear too small. This effect is strongest for high concentrations (0.075% v/v and 0.15% v/v shown).

It should be noted that the graphs shown apply to the example of charged colloidal silica spheres under very low ionic strength conditions. Equivalent conditions in aqueous samples would correspond to the mean particle distance being on the order of the Debye-Hückel screening length.

How can these "incorrect" sizes be avoided? They cannot - but a dilution check will confirm whether the size was influenced or not. Theoretically, typical molecules below 1% concentration should not be influenced unless the lack of electrostatic screening (i.e. no salt in the buffer) leads to a much stronger, longer-range interaction between the molecules.

References

[1] G. Grübel, D.L. Abernathy, D.O. Riese, W.L. Vos and G.H. Wegdam (2000) J. Appl. Cryst. 33, 424-427.

* For hard spheres the Percus-Yevick approximation exists for S(q), and H(q) has also been predicted for this 'ideal' case. For charged spheres, however, only numerical models exist.