流变学技术笔记——对流变学与粒子参数之间的相关性理解1



下载



流变学与粒子 参数之间的 相关性理解 

  微粒物质的物性受粒度分布和zeta 电位（测量粒子电荷）两者均对涂层物质的流变性产生影响。 试验结果涉及上述影响中的几种不同类型的涂层，流变性通过 Malvern Bohlin Gemini流变仪测量。粒径及 zeta 电位分别通过Malvern Mastersizer 2000 和 MalvernZetasizer Nano ZS 测量。

  本材料中使用的例子已考虑在大多数条件下非常普遍的情况，理论可以广泛应用于涂层体系。

  物质的“流动性”表现为其粘度或对流动的抵抗。当谈到某一特定物质的粘度时，重要的是要认识到粘度不仅仅表现为一个值，而是以剪切应力的函数形式体现。

  剪切应力为物质在受到 1s-1 以下小剪切应力或 100s-1 以上高剪切应力时的变形提供指标。

  表 1 中总结了与涂层物质相关的工艺及相应的剪切速率范围。

  考虑到剪切速率时，用于涂层的物质遵循以下类别。

– 稠度增厚（剪切速率增加时粘度增加的现象）；
– 牛顿流体（在所有剪切速率下保持恒定粘度的现象）；
– 稀化性（剪切速率增加时粘度减少的现象）；

粒径与流变学的关系

  首先需要考虑的事项是PSV（压敏胶：在室温条件下具有粘性并可通过轻微施压粘附的物质）的粘度。对于乳胶粒子而言，有两种不同尺寸。图 1 显示，随着粒径增大，PSA 的粘度显著降低。

  这仅仅是平均粒径变化产生的结果。体积百分比（或 PSA 中添加的乳胶的质量）是固定的。在给定的乳胶质量中，根据粒径不同，数量会有所不同。即，相比于 750 微米尺寸的乳胶，175 微米的乳胶粒子会更多。

  这是一般粒子间的相互作用，大颗粒物质中相互作用较少，这可能是机械的或电气/化学性相互作用。因此，在相同体积百分比中，小粒子存在的数量更多，相互作用也更多。

  当把相互作用考虑为短距离结构时，基本上是通过点度增加的方式测量到。剪切速率可作为变形因子，低剪切速率较高剪切速率带来的变形小。因此，弱力的低剪切速率与强力的高剪切速率是不同的。图 1 还显示，在低剪切速率下具有最大的粘度差异，这是因为粒子相互作用弱且易被破坏。

  因此这两个系统在高剪切速率下，粒子相互作用较少，所以呈现相似的粘度。

  如果是以树脂为基的墨水（使用滑石作填料的墨水），系统中粘度将会变化。图 2 中的墨水原液显示典型牛顿粘度。添加的树脂是相对坚硬的物质，因此这些高分子的相互作用显示为非常大的粘度，这些力表现为对剪切的抗力高聚物缠结，因此表现出最小的剪切稀化。

  对于 19 微米的滑石粒子来说，由于大尺寸粒子间的相对较小的相互作用，初始粘度表现出牛顿趋势，略有增加。然而，加入 5 微米小粒子时，由于粒子数量变多，因此粘度明显增加。再次强调，这种粒子相互作用通常是弱的。因此在低剪切速率下显示高粘度的剪切稀化。

体积百分比与分散度的影响

  迄今为止所提出的讨论了填料的常定体积百分比的情况。本质上是将相同的粒子引入系统中。简单地增加粒子的部分比例通常会在粘度计中测量的粘度增加。但是，如果在实际测量流变学时，粘度与剪切速率之间的关系需要更详细的信息。图 3显示，墨水的粘度在不同剪切速率下随着粒子体积百分比的增加而增加。然而流动性也会改变。

  一般来说，在低体积百分比（40% 以下）中，由于系统内粒子数量足够低，以致于彼此之间没有交互作用，因此仍然表现出牛顿特性。在 50% 左右时，粒子数量较多，彼此发生强相互作用，因此粘度增加。之前讨论过，这些相互作用可描述为弱，而在高剪切速率下，这些弱结构会被打破，呈现剪切稀化结果。

  体积分数超过 60% 的系统显然有更多的相互作用，并且在低剪切速率下表现出高粘度，显示剪切稀化行为。然而，还需考虑这些复杂系统中粒子运动的机械困难。这种情况在高剪切速率下尤为显著，表现为粘度增加。此时显示剪切增稠或胀大的特性。

  体积分数对粘度依赖性可通过 Krieger-Dougherty 方程表示。η 表示悬浮液的粘度，ηmedium 为基础溶剂的粘度。φ 为悬浮液中存在的固体物质的体积分数，φm 为体积分数的最大值。

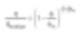
  此外，[η] 表示溶剂的固有粘度，若为球形粒子则值为 2.5。尽管 Krieger-Dougherty 方程即使在固定的体积百分比下，它也可以随着粒子的物性而改变。在此情况下，最大体积百分比（或填充）直接受到粒径分布或粒子间距的影响。对于单分散填充的系统，球形粒子的最大体积百分比略靠近 64%。但这同样也通过结构流动有效增加（即体积比低时）。“易流动”可以被简单地理解为粘度降低，这在更深层次上可以认为大的粒子运动因小粒子起到的有效润滑作用而促进。

  图 4 显示这个有趣的结果：在固定的体积量中，由大、小粒子构成的多分散系统的粘度可能低于各自的粘度值。这显示了两个相反的效果，一个是依赖于粒子尺寸的交互粒子数量，另一个是多分性效应。

  在涂层系统中，简单的增加多分散度或增加添加剂的量可以在添加填料或颜料后，在给定环境中保持粘度。

  多分散效应在不同供应商替换涂层材料的添加剂时需要考虑。由于供应商使用相同的粒径，因此不会影响分布。因此，流变学特性不会变化。例如，以 Mastersizer 2000 测量时可以测量粒径，也可以测量粒度分布。